Welcome to The Coding College, where we simplify coding and data science concepts for you! In this guide, we’ll delve into the Uniform Distribution, its features, and how to implement it using Python.
What is Uniform Distribution?
The Uniform Distribution is a probability distribution where all outcomes are equally likely within a specified range. This distribution can be:
- Discrete Uniform Distribution: Finite set of outcomes, each equally likely (e.g., rolling a die).
- Continuous Uniform Distribution: Continuous range of outcomes, each equally probable within an interval.
Probability Density Function (PDF):
For a continuous uniform distribution between a and b:
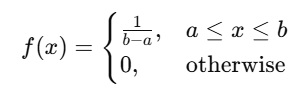
- a: Lower bound of the range.
- b: Upper bound of the range.
- f(x): Constant probability density within the range.
Real-Life Examples of Uniform Distribution
- Randomly selecting a number between 0 and 1.
- Rolling a fair die (discrete case).
- Randomly assigning tasks to workers with equal probability.
- Simulating fair outcomes in games or lotteries.
Uniform Distribution in NumPy
Python’s NumPy library provides tools to generate uniform random numbers for both continuous and discrete cases.
Functions:
- Continuous Uniform Distribution:
numpy.random.uniform(low=0.0, high=1.0, size=None)low: Lower bound of the range (inclusive).high: Upper bound of the range (exclusive).size: Number of random numbers to generate.- Discrete Uniform Distribution:
numpy.random.randint(low, high=None, size=None, dtype=int)- Generates random integers within a specified range.
Example 1: Generating Continuous Uniform Data
import numpy as np
# Generate random numbers from a uniform distribution
data = np.random.uniform(low=0, high=10, size=5)
print("Random numbers from uniform distribution:", data)Output (Example):
[2.345 6.789 3.456 7.123 9.876]Example 2: Generating Discrete Uniform Data
import numpy as np
# Generate random integers from a uniform distribution
data = np.random.randint(low=1, high=7, size=10) # Simulate rolling a die
print("Random integers from discrete uniform distribution:", data)Output (Example):
[4 6 2 5 3 1 6 4 2 5]Example 3: Visualizing Continuous Uniform Distribution
import numpy as np
import matplotlib.pyplot as plt
# Generate data
data = np.random.uniform(low=0, high=1, size=1000)
# Plot histogram
plt.hist(data, bins=20, color='skyblue', edgecolor='black')
plt.title('Uniform Distribution (0 to 1)')
plt.xlabel('Value')
plt.ylabel('Frequency')
plt.show()Example 4: Simulating a Real-World Scenario
Scenario: Random Task Assignment
Assign a random task ID to 5 employees from a list of tasks (1 to 10):
import numpy as np
# Assign random task IDs
tasks = np.random.randint(low=1, high=11, size=5)
print("Assigned tasks:", tasks)Comparing Uniform and Other Distributions
- Uniform vs. Normal Distribution:
- In a uniform distribution, all outcomes are equally probable.
- In a normal distribution, outcomes are concentrated around the mean.
- Uniform vs. Exponential Distribution:
- Exponential distribution models the time between events in a Poisson process.
- Uniform distribution assumes equal likelihood for all outcomes.
Applications of Uniform Distribution
- Simulation and Modeling: Simulate fair outcomes in games or random processes.
- Random Sampling: Generate data points for algorithms or experiments.
- Random Testing: Test systems with random inputs.
- Gaming: Model dice rolls, shuffling, or other random events.
Summary
The Uniform Distribution is a foundational concept in probability and statistics, representing scenarios where all outcomes are equally likely. With Python’s NumPy, you can generate both continuous and discrete uniform data, making it a valuable tool for simulation, random sampling, and more.