Perceptrons

Perceptrons are the fundamental building blocks of artificial neural networks, marking the origin of machine learning and deep learning models. Introduced in 1958 by Frank Rosenblatt, the perceptron is a type of artificial neuron used to classify data points into two categories. This article explores perceptrons, their architecture, working principles, and applications. For more in-depth coding and machine learning content, visit The Coding College.

What is a Perceptron?

A perceptron is a supervised learning algorithm used for binary classification. It mimics the functioning of biological neurons and can make decisions by learning weights assigned to input features.

Components of a Perceptron

  • Inputs (x1,x2,…,xn): Represent features of the dataset.
  • Weights (w1,w2,…,wn): Determine the influence of each input.
  • Bias (b): Shifts the decision boundary to improve flexibility.
  • Summation Function: Computes the weighted sum of inputs:
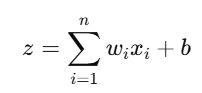
  • Activation Function: Determines the output based on zz. In a perceptron, this is usually a step function:

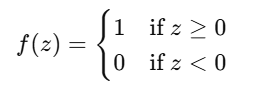
Perceptron Architecture

The perceptron architecture consists of:

  • Input Layer: Accepts data points as input.
  • Summation Node: Combines inputs with weights and bias.
  • Output Node: Produces the final prediction based on the activation function.
Perceptron Architecture

How Does a Perceptron Work?

  1. Initialize Weights and Bias: Start with random values.
  2. Input Data: Pass the feature values into the perceptron.
  3. Compute Weighted Sum: Calculate z=∑wixi+b.
  4. Apply Activation Function: Determine the output (1 or 0).
  5. Update Weights (Learning): Adjust weights and bias using the perceptron learning rule:
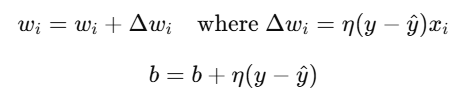
  1. y: Actual output.
  2. y^: Predicted output.
  3. η: Learning rate.

Limitations of Perceptrons

  1. Linear Separability: Perceptrons can only solve problems where the data is linearly separable, such as OR and AND gates. They fail for non-linear problems like XOR.
  2. Fixed Activation: The step function limits gradient-based optimization techniques.

Applications of Perceptrons

  1. Binary Classification
    • Example: Classifying emails as spam or not spam.
  2. Logic Gates
    • AND, OR, and NOT gates can be modeled using perceptrons.
  3. Feature Detection
    • Simple edge detection in image processing tasks.

Perceptrons in Python

Below is a simple Python implementation of a perceptron for a binary classification task:

import numpy as np

# Step Activation Function
def step_function(z):
    return 1 if z >= 0 else 0

# Perceptron Model
class Perceptron:
    def __init__(self, learning_rate=0.01, epochs=1000):
        self.lr = learning_rate
        self.epochs = epochs
        self.weights = None
        self.bias = None

    def fit(self, X, y):
        n_samples, n_features = X.shape
        self.weights = np.zeros(n_features)
        self.bias = 0

        for _ in range(self.epochs):
            for idx, x_i in enumerate(X):
                z = np.dot(x_i, self.weights) + self.bias
                y_pred = step_function(z)

                # Update weights and bias
                update = self.lr * (y[idx] - y_pred)
                self.weights += update * x_i
                self.bias += update

    def predict(self, X):
        linear_output = np.dot(X, self.weights) + self.bias
        return [step_function(i) for i in linear_output]

# Dataset: OR Gate
X = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
y = np.array([0, 1, 1, 1])

# Train Perceptron
model = Perceptron(learning_rate=0.1, epochs=1000)
model.fit(X, y)

# Predict
predictions = model.predict(X)
print("Predictions:", predictions)

Moving Beyond Perceptrons: Multi-Layer Perceptrons (MLPs)

The limitations of perceptrons led to the development of multi-layer perceptrons (MLPs), which form the basis of modern neural networks. MLPs overcome non-linear problems using multiple layers and activation functions like ReLU and sigmoid.

Leave a Comment