Linear Algebra

Linear Algebra is a foundational branch of mathematics that provides the tools to represent, manipulate, and analyze data in Machine Learning (ML). Its concepts are integral to data representation, transformations, and computations in ML algorithms.

This article explores the key concepts of linear algebra and their applications in Machine Learning.

Why is Linear Algebra Important in Machine Learning?

Machine Learning models rely on processing data in structured forms. Linear Algebra provides:

1. Data Representation: Vectors and matrices efficiently represent data and model parameters.
2. Transformations: Operations like scaling, rotation, and projection are expressed mathematically using matrices.
3. Algorithm Design: Core ML algorithms like gradient descent, support vector machines, and neural networks are built upon linear algebra operations.
4. Dimensionality Reduction: Techniques like Principal Component Analysis (PCA) rely on eigenvalues and eigenvectors.

Key Concepts of Linear Algebra

1. Scalars, Vectors, Matrices, and Tensors

These are the building blocks of linear algebra in ML:

• Scalar: A single number (e.g., x=5).
• Vector: A 1D array of numbers (e.g., v=[2,3,5]).
• Matrix: A 2D array of numbers (e.g., A=[[1,2],[3,4]]).
• Tensor: A multi-dimensional array, generalizing matrices to higher dimensions.

Example: Data Representation

In ML, datasets are often represented as matrices, where rows are data points and columns are features.

2. Vector Operations

Vectors are fundamental in ML, representing data points, weights, or predictions.

Operations:

• Addition/Subtraction: Combine vectors element-wise.
• Dot Product: Measures similarity between two vectors.

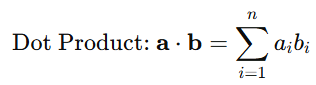
• Norm: Represents the magnitude of a vector.

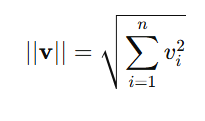
Application:

The dot product is used in classification algorithms like logistic regression and neural networks.

3. Matrix Operations

Matrices store and manipulate multi-dimensional data.

Operations:

• Addition/Subtraction: Element-wise combination.
• Matrix Multiplication: Combines two matrices.

C=A⋅B

• Transpose: Flips rows and columns of a matrix.

AT

• Inverse: A matrix A has an inverse A^{-1} such that A⋅A−1=I, where I is the identity matrix.

Application:

Matrix multiplication is widely used in deep learning for layer computations.

4. Determinants and Eigenvalues

• Determinants: Measure the “volume scaling factor” of a matrix and help determine if a matrix is invertible.
• Eigenvalues and Eigenvectors: Key in dimensionality reduction and feature extraction.

Application:

Principal Component Analysis (PCA) uses eigenvalues and eigenvectors to identify the principal components of data.

5. Linear Transformations

Linear transformations map vectors from one space to another while preserving the operations of addition and scalar multiplication.

Example:

In ML, linear transformations are used to scale and rotate data, ensuring algorithms can process it effectively.

Applications of Linear Algebra in Machine Learning

1. Linear Regression
   Predicts outcomes using a linear relationship between features and targets. y=X⋅w+b
2. Neural Networks
   Represent weights, activations, and outputs as matrices and tensors for efficient computation.
3. Dimensionality Reduction
   PCA reduces high-dimensional data to its most significant components using eigenvectors.
4. Natural Language Processing (NLP)
   Word embeddings like Word2Vec and GloVe represent words as vectors.
5. Computer Vision
   Images are represented as matrices of pixel values, manipulated using linear algebra operations.

Learning Resources for Linear Algebra

1. Books
   • Linear Algebra and Its Applications by Gilbert Strang.
   • Introduction to Linear Algebra by Gilbert Strang.
2. Online Courses
   • Mathematics for Machine Learning (Coursera).
   • Linear Algebra Refresher (Khan Academy).
3. Tools
   • Python Libraries: NumPy and SciPy for implementing linear algebra operations.
   • MATLAB: A robust tool for linear algebra computations.