Matrices are a cornerstone of mathematics and a fundamental tool in Machine Learning (ML). They provide a structured way to represent and manipulate data, perform calculations, and enable efficient computations. This article explores matrices, their operations, and applications in ML.
What is a Matrix?
A matrix is a rectangular array of numbers arranged in rows and columns. It is denoted as:

Where A has m rows and nn columns, making it an m×n matrix.
Types of Matrices
- Row Matrix: A matrix with one row (1×n).
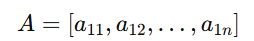
- Column Matrix: A matrix with one column (m×1).
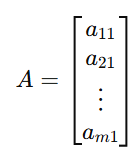
- Square Matrix: A matrix where the number of rows equals the number of columns (n×n).
- Identity Matrix: A square matrix with 1s on the diagonal and 0s elsewhere.
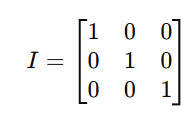
- Diagonal Matrix: A square matrix where all non-diagonal elements are 0.
- Zero Matrix: A matrix with all elements equal to 0.
Matrix Operations
1. Matrix Addition and Subtraction
Performed element-wise between matrices of the same dimensions.
Application:
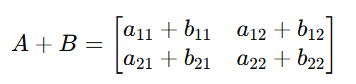
Used in updating weights in ML models during optimization.
2. Scalar Multiplication
Each element of the matrix is multiplied by a scalar value.
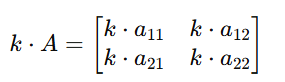
Application:
Scaling data or model parameters.
3. Matrix Multiplication
The dot product of rows in the first matrix and columns in the second.
For A(m×n) and B(n×p):
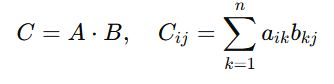
Application:
Used in transforming data, combining layers in neural networks, and linear regression.
4. Transpose of a Matrix
Flips a matrix over its diagonal.
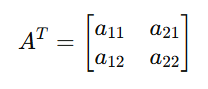
Application:
Used in covariance matrices and certain optimization algorithms.
5. Matrix Determinant
A scalar value that represents a square matrix’s properties.
For A(2×2): det(A)=a11a22−a12a21
Application:
Determines if a matrix is invertible and used in linear transformations.
6. Matrix Inverse
The inverse of A (A^{-1}) satisfies A⋅A−1=I.
For A(2×2):
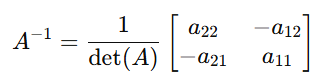
Application:
Used in solving systems of linear equations.
7. Eigenvalues and Eigenvectors
For a square matrix A, an eigenvector vv satisfies:
A⋅v=λ⋅v
Where λ is the eigenvalue.
Application:
Dimensionality reduction techniques like PCA use eigenvalues and eigenvectors.
Applications of Matrices in Machine Learning
- Data Representation
- Datasets are often represented as matrices where rows are data points and columns are features.
- Linear Transformations
- Matrices are used to scale, rotate, and project data.
- Neural Networks
- Weight matrices are multiplied with input vectors to compute outputs.
- Dimensionality Reduction
- Matrices of eigenvectors are used to project data into lower dimensions.
- Image Processing
- Images are represented as pixel matrices, enabling manipulations like filtering and transformations.
- Recommender Systems
- Matrices are used to represent user-item interactions for collaborative filtering.
Learning Matrices with Python
Python libraries like NumPy and TensorFlow make matrix operations simple.
Example: Matrix Multiplication
import numpy as np
A = np.array([[1, 2], [3, 4]])
B = np.array([[5, 6], [7, 8]])
C = np.dot(A, B)
print(C)Learning Resources
- Books
- Introduction to Linear Algebra by Gilbert Strang.
- Linear Algebra and Its Applications by David C. Lay.
- Online Courses
- Mathematics for Machine Learning (Coursera).
- Linear Algebra (Khan Academy).
- Visualization Tools
- Use
MatplotliborPlotlyfor visualizing matrix transformations.
- Use