Welcome to TheCodingCollege.com! In this post, we’ll explore Memoization, a core concept in Data Structures and Algorithms (DSA). You’ll learn what memoization is, how it works, why it’s useful, and see examples of its implementation in Python.
What is Memoization?
Memoization is an optimization technique used to improve the performance of algorithms by storing the results of expensive function calls and reusing them when the same inputs occur again.
Key Characteristics:
- Dynamic Programming: Memoization is a top-down approach to dynamic programming.
- Reduces Redundancy: Avoids recalculating results for previously solved subproblems.
- Space-Time Tradeoff: Utilizes additional memory to save computation time.
Real-World Analogy:
Imagine a student preparing for exams. Instead of repeatedly studying the same topic from scratch, they make notes (store results) and refer to them when needed, saving time.
Why Use Memoization?
- Improves Performance:
Memoization drastically reduces the time complexity of recursive algorithms. - Simplifies Recursion:
By reusing results, recursive functions avoid redundant calls, making them more efficient. - Avoids Recomputations:
Saves results for overlapping subproblems in algorithms like the Fibonacci series or knapsack problem.
How Does Memoization Work?
- Check Cache: Before performing a computation, check if the result is already stored.
- Perform Calculation: If not stored, compute the result.
- Store Result: Save the computed result for future use.
- Reuse: Return the cached result when the same input is encountered again.
Memoization vs Tabulation
| Feature | Memoization | Tabulation |
|---|---|---|
| Approach | Top-down (recursive) | Bottom-up (iterative) |
| Storage | Results stored during recursion | Table filled iteratively |
| Space Efficiency | May use more stack memory for recursion | Generally more stack-efficient |
| Ease of Implementation | Easier for problems naturally recursive | May require problem restructuring |
Example: Fibonacci Series with Memoization
Naive Recursive Approach
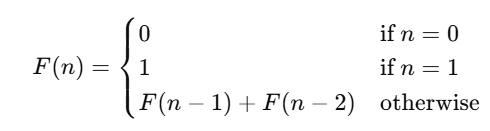
def fibonacci(n):
if n == 0:
return 0
if n == 1:
return 1
return fibonacci(n - 1) + fibonacci(n - 2)
# Example Usage
print(fibonacci(10)) # Output: 55Issue: Exponential Time Complexity O(2^n).
Optimized with Memoization
def fibonacci_memo(n, memo={}):
if n in memo:
return memo[n]
if n == 0:
return 0
if n == 1:
return 1
memo[n] = fibonacci_memo(n - 1, memo) + fibonacci_memo(n - 2, memo)
return memo[n]
# Example Usage
print(fibonacci_memo(10)) # Output: 55Analysis:
- Time Complexity: O(n).
- Space Complexity: O(n) for the memo dictionary.
Applications of Memoization
- Dynamic Programming Problems:
- Fibonacci Series
- 0/1 Knapsack Problem
- Longest Common Subsequence
- Game Theory:
Solving games with recursive state evaluations. - Optimization Problems:
Problems with overlapping subproblems, like matrix chain multiplication.
Advantages of Memoization
- Efficiency: Reduces redundant calculations.
- Ease of Debugging: Recursive functions are often easier to understand and debug.
- Scalability: Handles large inputs effectively with reduced time complexity.
Disadvantages of Memoization
- Space Requirements:
Requires additional memory to store computed results. - Stack Overflow:
Recursive calls may lead to stack overflow for extremely deep recursions. - Complexity in Some Cases:
Not all problems lend themselves easily to memoization.
Conclusion
Memoization is a powerful optimization technique that improves the performance of recursive algorithms. By storing and reusing results, it helps solve computationally intensive problems efficiently.