Vectors are one of the most fundamental concepts in mathematics, forming the basis for data representation in Machine Learning (ML). They enable models to process, analyze, and learn from data effectively. This article delves into what vectors are, their operations, and their applications in ML.
What Are Vectors?
A vector is a mathematical entity that has both magnitude and direction. In the context of ML, vectors are used to represent data points, weights, or any structured data in a numerical format.
- Example: A 3-dimensional vector: v=[v1,v2,v3]
- Here, v1, v2, and v3 are the vector’s components.
Types of Vectors in ML
- Row Vector: A 1xnn matrix (horizontal arrangement). v=[v1,v2,…,vn]
- Column Vector: A nnx1 matrix (vertical arrangement).
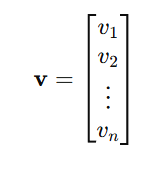
Vector Operations
1. Vector Addition and Subtraction
Combine or subtract vectors element-wise.
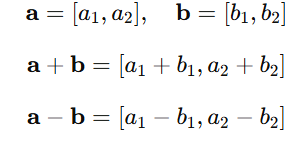
Application:
Addition and subtraction are used to compute gradients in optimization problems.
2. Scalar Multiplication
Multiply each vector component by a scalar value.
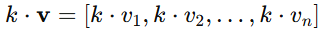
Application:
Scalar multiplication is used in scaling features or updating weights in ML models.
3. Dot Product
Measures the similarity between two vectors.
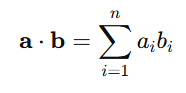
Example:
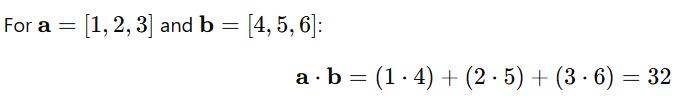
Application:
Dot products are used in measuring similarity, such as in recommendation systems and classification.
4. Cross Product
Produces a vector orthogonal to the given vectors (only in 3D space).
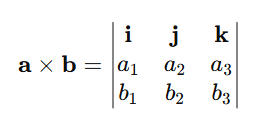
5. Norm (Magnitude)
The length or size of a vector.
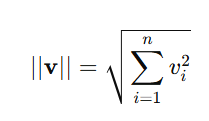
Application:
Used to normalize vectors, ensuring consistent scales across features.
6. Projection
Projects one vector onto another.

Application:
Projection is essential in understanding relationships between data dimensions.
Applications of Vectors in Machine Learning
- Data Representation
- Features of a dataset are often represented as vectors.
- Example: Representing a house as a vector of its features: [size,rooms,price][ \text{size}, \text{rooms}, \text{price} ].
- Weights and Bias in Models
- In neural networks, weights and biases are vectors used for linear transformations.
- Distance Metrics
- Distance between two vectors (a\mathbf{a} and b\mathbf{b}) is calculated to measure similarity.
- Gradient Descent
- Gradients are vectors that guide optimization in ML.
- Natural Language Processing (NLP)
- Word embeddings represent words as high-dimensional vectors.
Visualizing Vectors
Vectors can be visualized as arrows in space, starting from the origin. Their direction and length indicate their orientation and magnitude.
Example:
In a 2D plane, v=[3,4] is represented as an arrow from [0,0] to [3,4].
Learning Resources
- Books
- Linear Algebra and Its Applications by Gilbert Strang.
- Introduction to Linear Algebra by Gilbert Strang.
- Online Resources
- Khan Academy: Linear Algebra tutorials.
- 3Blue1Brown: Visual explanations of vector mathematics.
- Python Libraries
- Use
NumPyto perform vector operations programmatically.
- Use