Welcome to The Coding College, your trusted resource for coding tutorials and programming knowledge. In this post, we will explore Linear Functions, a key concept in Data Science and Machine Learning. Understanding linear functions is crucial for building predictive models, especially in techniques like linear regression. Let’s break down what linear functions are, how they are used in data science, and how you can implement them in your models.
What are Linear Functions?
A linear function is a mathematical function in which the relationship between the independent variable (or input) and the dependent variable (or output) is linear. In simpler terms, this means that the function forms a straight line when graphed. The general form of a linear function is: y=mx+by = mx + b
Where:
- yy is the dependent variable (the output).
- xx is the independent variable (the input).
- mm is the slope of the line, which represents the rate of change.
- bb is the y-intercept, which represents the point where the line intersects the y-axis.
In data science, linear functions are often used to model relationships between variables, especially in linear regression, which is a foundational technique in machine learning.
Importance of Linear Functions in Data Science
Linear functions play a key role in several areas of Data Science, including:
- Linear Regression: Linear functions form the basis of linear regression, one of the simplest and most widely used statistical models in machine learning. It helps predict the value of a dependent variable based on one or more independent variables.
- Predictive Modeling: Linear models are often used for prediction when the relationship between variables is approximately linear. For example, predicting a person’s salary based on years of experience is a typical case of linear regression.
- Feature Relationship Analysis: Linear functions help data scientists understand how different features (input variables) are related to each other. For example, understanding how customer age and income correlate can provide valuable insights for targeted marketing.
How Linear Functions Work in Data Science
Let’s explore how linear functions are applied in data science. The most common application of linear functions is in linear regression, where the goal is to model the relationship between a dependent variable and one or more independent variables.
In simple linear regression, the goal is to fit a straight line to a dataset, such that the error (difference between predicted and actual values) is minimized. The equation for a simple linear regression model is:
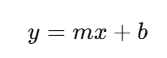
Where:
- y is the predicted value (output),
- x is the input feature,
- m is the model’s slope (coefficient), and
- b is the y-intercept (constant term).
In multiple linear regression, where there are multiple independent variables, the equation becomes:
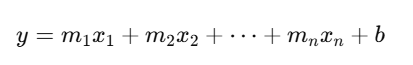
Where:
- x1,x2,…,xn are the input features,
- m1,m2,…,mnm_1, m_2, \dots, m_nm1,m2,…,mn are the coefficients (slopes) for each feature.
Example: Implementing Linear Regression with Python
To understand how linear functions work in practice, let’s implement Linear Regression using Python and the popular library scikit-learn. This example will demonstrate how we can fit a linear function to a dataset and use it for prediction.
import numpy as np
import pandas as pd
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt
# Sample data: Years of experience vs Salary
data = {
'Experience': [1, 2, 3, 4, 5, 6, 7, 8, 9, 10],
'Salary': [40000, 45000, 50000, 55000, 60000, 65000, 70000, 75000, 80000, 85000]
}
df = pd.DataFrame(data)
# Define the independent variable (X) and dependent variable (y)
X = df[['Experience']]
y = df['Salary']
# Initialize the Linear Regression model
model = LinearRegression()
# Fit the model
model.fit(X, y)
# Predict salary for a person with 6 years of experience
predicted_salary = model.predict([[6]])
print(f"Predicted salary for 6 years of experience: {predicted_salary[0]}")
# Plotting the data and the linear regression line
plt.scatter(X, y, color='blue') # Data points
plt.plot(X, model.predict(X), color='red') # Regression line
plt.xlabel('Years of Experience')
plt.ylabel('Salary')
plt.title('Linear Regression: Salary vs Experience')
plt.show()In this example, we use the LinearRegression model from scikit-learn to fit a linear function to the dataset, predict the salary for a person with 6 years of experience, and visualize the data points along with the regression line.
Advantages of Linear Functions in Data Science
- Simplicity: Linear models are easy to understand and interpret. They are a great starting point for many data analysis problems.
- Computational Efficiency: Linear functions require minimal computational resources and are relatively fast to train.
- Transparency: Since the relationship between variables is straightforward (a straight line), the results of linear models are easy to explain to stakeholders.
Limitations of Linear Functions
While linear functions are powerful and widely used, they have limitations:
- Linearity Assumption: Linear models assume a linear relationship between input features and the target variable. If the data is non-linear, a linear function may not provide accurate predictions.
- Sensitivity to Outliers: Linear models are sensitive to outliers, and a few extreme data points can significantly affect the slope of the line.
- Over-simplification: In some cases, using a linear model may oversimplify the problem and ignore important complexities in the data.
Conclusion
In Data Science, understanding Linear Functions is fundamental to building accurate predictive models. Linear regression, which uses these functions, is a simple yet effective technique for predicting outcomes based on historical data. By grasping the principles of linear functions, data scientists can better model relationships between variables and make more informed predictions.
At The Coding College, we’re committed to helping you master the key concepts in Data Science. Stay tuned for more tutorials on regression techniques, machine learning algorithms, and much more!