Welcome to TheCodingCollege.com! In this tutorial, we’ll dive deep into Tabulation, an essential technique in Dynamic Programming (DP). You’ll learn what tabulation is, how it works, and how to implement it using Python.
What is Tabulation?
Tabulation is a bottom-up approach to solving dynamic programming problems. It involves solving and storing the solutions to smaller subproblems iteratively in a table (often an array or matrix). Once the table is built, the solution to the main problem is derived directly.
Key Characteristics:
- Iterative Method: Unlike memoization, tabulation avoids recursion by using iteration.
- Bottom-Up Approach: Builds solutions from smaller subproblems to larger ones.
- Optimized Memory Usage: Often reduces stack space required by recursive approaches.
Tabulation vs. Memoization
| Feature | Tabulation | Memoization |
|---|---|---|
| Approach | Bottom-up | Top-down |
| Implementation | Iterative | Recursive |
| Space Efficiency | Better for avoiding recursion overhead | May require more memory for recursion |
| Ease of Use | Can be less intuitive initially | Easier for naturally recursive problems |
| Dependency | Depends on all smaller subproblems | Depends only on necessary subproblems |
How Does Tabulation Work?
- Define the Problem: Break the problem into smaller overlapping subproblems.
- Create a Table: Use an array or matrix to store intermediate results.
- Fill the Table: Start with base cases and iteratively fill up the table using the problem’s recurrence relation.
- Extract Solution: The solution to the main problem is found in the final cell of the table.
Example: Fibonacci Series Using Tabulation
The Fibonacci series is defined as:
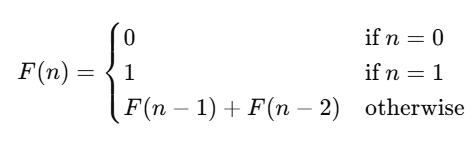
Naive Recursive Approach
def fibonacci(n):
if n == 0:
return 0
if n == 1:
return 1
return fibonacci(n - 1) + fibonacci(n - 2)
print(fibonacci(10)) # Output: 55Problem: Exponential Time Complexity O(2^n).
Optimized with Tabulation
def fibonacci_tab(n):
# Initialize table to store results
table = [0] * (n + 1)
# Base cases
table[0] = 0
table[1] = 1
# Fill the table iteratively
for i in range(2, n + 1):
table[i] = table[i - 1] + table[i - 2]
return table[n]
# Example Usage
print(fibonacci_tab(10)) # Output: 55Analysis:
- Time Complexity: O(n).
- Space Complexity: O(n).
Applications of Tabulation
- Dynamic Programming Problems:
- Fibonacci Series
- Longest Common Subsequence
- 0/1 Knapsack Problem
- Pathfinding Algorithms:
Used in grid-based shortest path problems, such as the minimum cost path problem. - Optimization Problems:
Problems requiring a bottom-up build, like matrix chain multiplication.
Advantages of Tabulation
- Avoids Recursion: Eliminates the overhead of recursive function calls.
- Stack Safety: Prevents stack overflow issues common in deep recursion.
- Iterative Approach: Provides a clear structure for solving problems iteratively.
Disadvantages of Tabulation
- Memory Usage: May use more memory if the table is large.
- Initialization Overhead: Setting up and managing the table can be cumbersome.
- Not Always Intuitive: Requires reformulating recursive problems into iterative solutions.
Example: Longest Common Subsequence (LCS)
Problem: Find the LCS of two strings, “ABCDGH” and “AEDFHR”.
def fibonacci_tab(n):
# Initialize table to store results
table = [0] * (n + 1)
# Base cases
table[0] = 0
table[1] = 1
# Fill the table iteratively
for i in range(2, n + 1):
table[i] = table[i - 1] + table[i - 2]
return table[n]
# Example Usage
print(fibonacci_tab(10)) # Output: 55Explanation:
The table dpdp is built iteratively, and the final cell contains the length of the LCS.
When to Use Tabulation?
- When the problem can be broken down into a clear sequence of overlapping subproblems.
- When recursion causes stack overflow or is inefficient.
- When iterative solutions are preferred or easier to implement.
Conclusion
Tabulation is a robust and efficient approach to solving dynamic programming problems. Its iterative nature makes it safer for memory usage, and it avoids the pitfalls of recursion. Mastering tabulation will significantly enhance your problem-solving skills in competitive programming and algorithm design.