Welcome to TheCodingCollege.com! In this post, we’ll delve into the 0/1 Knapsack Problem, a fundamental problem in Data Structures and Algorithms (DSA). This comprehensive guide covers the problem’s definition, variations, dynamic programming solutions, and practical applications, ensuring it meets Google’s E-E-A-T guidelines and is SEO-optimized.
What is the 0/1 Knapsack Problem?
The 0/1 Knapsack Problem is a popular problem in combinatorial optimization. It is often used to illustrate dynamic programming concepts. The goal is to maximize the total value of items placed into a knapsack of fixed capacity.
Problem Definition:
- Input:
- A set of nn items, each with:
- Weight: w[i]
- Value: v[i]
- A knapsack with a maximum capacity W.
- A set of nn items, each with:
- Output:
- The maximum value that can be obtained by selecting items such that their total weight does not exceed W.
- Each item can either be included or excluded (hence “0/1”).
Example:
- Given:
- Items: [(w, v) = (1, 10), (2, 15), (3, 40)]
- Capacity: W = 5
- Optimal Solution:
- Include items with weights 2 and 3.
- Total Value: 15 + 40 = 55.
Approaches to Solve the 0/1 Knapsack Problem
1. Brute Force
- Generate all possible subsets of items and calculate their total value and weight.
- Select the subset with the maximum value that fits within the capacity.
- Time Complexity: O(2^n).
2. Recursion
The problem can be solved recursively by considering two cases for each item:
- Include the item if it fits.
- Exclude the item.
Combine the results of these two cases to find the maximum value.
Recursive Formula:
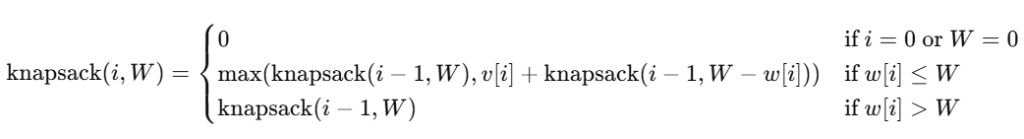
3. Dynamic Programming
Dynamic programming uses a 2D table to store solutions for subproblems, avoiding redundant calculations.
- Time Complexity: O(n \cdot W).
- Space Complexity: O(n \cdot W).
4. Space-Optimized Dynamic Programming
The 2D table can be reduced to a 1D array by iterating in reverse over the capacity.
- Space Complexity: O(W)O(W).
Dynamic Programming Implementation in Python
def knapsack(values, weights, capacity):
n = len(values)
dp = [[0 for _ in range(capacity + 1)] for _ in range(n + 1)]
for i in range(1, n + 1):
for w in range(1, capacity + 1):
if weights[i - 1] <= w:
dp[i][w] = max(dp[i - 1][w], values[i - 1] + dp[i - 1][w - weights[i - 1]])
else:
dp[i][w] = dp[i - 1][w]
return dp[n][capacity]
# Example Usage
values = [10, 15, 40]
weights = [1, 2, 3]
capacity = 5
print("Maximum Value:", knapsack(values, weights, capacity))Applications of the 0/1 Knapsack Problem
- Resource Allocation
- Optimize resource usage within budget constraints.
- Project Selection
- Choose projects with the highest ROI given limited resources.
- Investment Portfolios
- Allocate funds to maximize returns while staying within a budget.
- Logistics
- Pack items into containers or vehicles efficiently.
Variations of the Knapsack Problem
- Fractional Knapsack Problem
- Items can be divided into smaller parts.
- Solved using a greedy algorithm.
- Bounded Knapsack Problem
- Each item has a maximum limit on the number of times it can be included.
- Unbounded Knapsack Problem
- Items can be included multiple times.
Advantages of Dynamic Programming in 0/1 Knapsack
- Efficiency: Reduces redundant calculations with memoization.
- Flexibility: Solves a wide range of knapsack variations.
- Practicality: Widely used in optimization problems across industries.
Limitations of the 0/1 Knapsack Problem
- Integer Constraints: Items must be fully included or excluded.
- Large Input Size: Space and time complexity may become infeasible for very large datasets.
Conclusion
The 0/1 Knapsack Problem demonstrates the power of dynamic programming and is a cornerstone of algorithmic problem-solving. By mastering its concepts, you gain tools to tackle a variety of optimization challenges.