Math for Machine Learning Tutorial

Understanding the mathematics behind machine learning is essential for developing algorithms, interpreting models, and solving complex problems. In this tutorial, we’ll cover the key mathematical concepts and their applications in machine learning. At The Coding College, our goal is to simplify complex topics for beginners and experienced learners alike.

Why Math is Important in Machine Learning?

Math forms the foundation of machine learning algorithms. It helps in:

1. Understanding Model Behavior: Gain insights into how algorithms work under the hood.
2. Optimizing Models: Use mathematical techniques to improve model accuracy and efficiency.
3. Making Informed Decisions: Interpret the results and validate their reliability.

Key areas of math used in machine learning include linear algebra, calculus, probability, statistics, and optimization.

1. Linear Algebra

Linear algebra is at the core of most machine learning models, particularly deep learning.

• Key Concepts:
  • Vectors and Matrices
  • Matrix Multiplication
  • Eigenvalues and Eigenvectors
  • Singular Value Decomposition (SVD)
• Applications:
  • Representing datasets as matrices
  • Performing transformations in neural networks
  • Reducing dimensionality with techniques like PCA

2. Calculus

Calculus is crucial for understanding how machine learning models learn.

• Key Concepts:
  • Derivatives and Gradients
  • Partial Derivatives
  • Chain Rule
  • Gradient Descent
• Applications:
  • Optimizing cost functions
  • Calculating updates in neural network weights

3. Probability and Statistics

Probability and statistics are used to model uncertainty and make predictions.

• Key Concepts:
  • Probability Distributions
  • Bayes’ Theorem
  • Expectation and Variance
  • Hypothesis Testing
• Applications:
  • Modeling uncertainty in predictions
  • Bayesian inference
  • Evaluating model performance with statistical tests

4. Optimization

Optimization is about finding the best parameters for a model.

• Key Concepts:
  • Convex Functions
  • Gradient Descent Variants (e.g., SGD, Adam)
  • Lagrange Multipliers
• Applications:
  • Minimizing loss functions
  • Convergence of machine learning models

5. Algorithms and Geometry

Geometry and algorithmic thinking are critical for understanding clustering, classification, and other tasks.

• Key Concepts:
  • Distance Metrics (Euclidean, Manhattan, etc.)
  • Hyperplanes and Decision Boundaries
  • Transformations
• Applications:
  • k-Nearest Neighbors (k-NN)
  • Support Vector Machines (SVMs)
  • Dimensionality reduction

Building a Machine Learning Model with Math

Here’s a step-by-step outline:

1. Define the Problem: Understand the data and identify the target outcome.
2. Prepare the Data: Use linear algebra to preprocess and clean the dataset.
3. Choose a Model: Select a suitable algorithm based on the problem type.
4. Train the Model: Use calculus and optimization to minimize the cost function.
5. Evaluate the Model: Apply probability and statistics to assess performance.
6. Optimize the Model: Fine-tune parameters to improve accuracy.

Practical Example: Linear Regression

Linear regression uses the following equation:

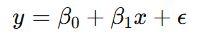
• Step 1: Use linear algebra to calculate the weights (β0,β1).
• Step 2: Apply calculus to minimize the cost function (e.g., Mean Squared Error).
• Step 3: Use statistics to interpret the goodness of fit (R-squared value).

Resources for Learning Math for Machine Learning

• Books:
  • “Mathematics for Machine Learning” by Deisenroth, Faisal, and Ong
  • “Deep Learning” by Ian Goodfellow
• Courses:
  • Linear Algebra by Khan Academy
  • Mathematics for Machine Learning by Coursera
• Tools:
  • Python Libraries: NumPy, SciPy, and Matplotlib for calculations and visualizations

Conclusion

Math is not just a prerequisite but a tool that empowers you to create better machine learning solutions. By mastering the mathematical concepts outlined in this tutorial, you’ll be better equipped to design, interpret, and optimize models.