Machine Learning (ML) relies on mathematics to develop models that analyze data, make predictions, and solve complex problems. Understanding the mathematical concepts behind ML equips developers and data scientists to build efficient algorithms and interpret their results accurately.
This article explores the critical mathematical foundations of Machine Learning, including linear algebra, calculus, probability, statistics, and optimization.
Why Mathematics is Essential in Machine Learning
Machine Learning algorithms process vast amounts of data, extract patterns, and make decisions. Mathematics provides the tools to:
- Represent and manipulate data effectively.
- Train models through optimization techniques.
- Interpret relationships between variables.
- Quantify uncertainty and validate models.
By grasping ML mathematics, practitioners can:
- Understand how algorithms work under the hood.
- Debug and improve ML models.
- Customize existing methods for specific problems.
Key Mathematical Foundations in Machine Learning
1. Linear Algebra
Linear algebra provides the language for ML. It is essential for data representation and model computation.
Key Concepts:
- Vectors: Represent data points and weights.
- Matrices: Store datasets and transformations.
- Dot Product: Measures similarity between vectors.
- Eigenvalues and Eigenvectors: Used in Principal Component Analysis (PCA) for dimensionality reduction.
Example:
A dataset with features can be represented as a matrix X where rows are data points, and columns are features. Linear transformations simplify the data for algorithms to process efficiently.
2. Calculus
Calculus is crucial for optimizing ML models by minimizing loss functions.
Key Concepts:
- Derivatives: Measure the rate of change.
- Gradient: A vector pointing in the direction of steepest ascent or descent.
- Partial Derivatives: Used for functions with multiple variables.
- Chain Rule: Fundamental for backpropagation in neural networks.
Example:
Gradient Descent uses derivatives to update model parameters:
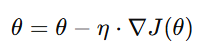
Where θ\theta are model parameters, η is the learning rate, and ∇J(θ) is the gradient of the loss function.
3. Probability and Statistics
Probability and statistics help ML models handle uncertainty and make inferences.
Key Concepts:
- Probability Distributions: Describe how data is distributed.
- Bayes’ Theorem: Foundation for probabilistic models.
- Random Variables: Represent outcomes of experiments.
- Hypothesis Testing: Validates model predictions.
Example:
In a classification task, the model predicts probabilities for different classes, choosing the class with the highest probability.
4. Optimization
Optimization ensures that ML models perform their best by finding the best parameters.
Key Concepts:
- Convex Optimization: Ensures global minima for loss functions.
- Gradient Descent: Iterative optimization technique.
- Stochastic Gradient Descent (SGD): Faster optimization using a subset of data at each step.
- Regularization: Prevents overfitting by adding a penalty term to the loss function.
Example:
Regularized Loss Function:
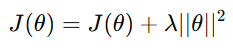
Where λ\lambda controls the penalty and ∣∣θ∣∣2 is the squared magnitude of parameters.
5. Discrete Mathematics
Discrete math is used in algorithms and data structures for ML.
Key Concepts:
- Graph Theory: Powers algorithms like recommendation systems.
- Boolean Algebra: Basis for decision trees.
- Combinatorics: Helps in feature selection and model evaluation.
Example:
Graph-based ML uses graph structures to model relationships between entities, such as social networks or recommendation systems.
Tools for Learning ML Mathematics
- Books
- Linear Algebra and Its Applications by Gilbert Strang.
- Probability and Statistics for Machine Learning by José Unpingco.
- Online Courses
- Mathematics for Machine Learning (Coursera).
- Introduction to Linear Algebra (MIT OpenCourseWare).
- Software
- Python Libraries: NumPy, SciPy, and Matplotlib for practical applications.
- Tools like TensorFlow and PyTorch for mathematical operations in ML.