Welcome to The Coding College, your go-to resource for coding tutorials! In this article, we dive into NumPy’s hyperbolic functions, which are essential for mathematical computations involving hyperbolas, exponential growth, and modeling natural processes. NumPy provides efficient and optimized implementations for hyperbolic functions, making it a preferred choice for scientific and numerical computing.
What Are Hyperbolic Functions?
Hyperbolic functions are analogs of trigonometric functions but are based on hyperbolas instead of circles. They are defined using exponential functions and are widely used in engineering, physics, and mathematics for applications like waveforms, catenary curves, and relativity.
Overview of NumPy Hyperbolic Functions
NumPy provides the following hyperbolic functions:
1. Basic Hyperbolic Functions
np.sinh(): Hyperbolic sinenp.cosh(): Hyperbolic cosinenp.tanh(): Hyperbolic tangent
2. Inverse Hyperbolic Functions
np.arcsinh(): Inverse hyperbolic sine (area hyperbolic sine)np.arccosh(): Inverse hyperbolic cosine (area hyperbolic cosine)np.arctanh(): Inverse hyperbolic tangent (area hyperbolic tangent)
Examples of NumPy Hyperbolic Functions
Example 1: Basic Hyperbolic Functions
import numpy as np
values = np.array([0, 1, -1])
# Hyperbolic sine, cosine, and tangent
sinh_values = np.sinh(values)
cosh_values = np.cosh(values)
tanh_values = np.tanh(values)
print("Hyperbolic Sine:", sinh_values)
print("Hyperbolic Cosine:", cosh_values)
print("Hyperbolic Tangent:", tanh_values)Output:
Hyperbolic Sine: [ 0. 1.17520119 -1.17520119]
Hyperbolic Cosine: [1. 1.54308063 1.54308063]
Hyperbolic Tangent: [ 0. 0.76159416 -0.76159416]Example 2: Inverse Hyperbolic Functions
# Inverse hyperbolic functions
values = np.array([0, 1, 2])
arcsinh_values = np.arcsinh(values)
arccosh_values = np.arccosh(values + 1) # arccosh is valid for x >= 1
arctanh_values = np.arctanh(np.array([0.5, -0.5]))
print("Inverse Hyperbolic Sine:", arcsinh_values)
print("Inverse Hyperbolic Cosine:", arccosh_values)
print("Inverse Hyperbolic Tangent:", arctanh_values)Output:
Inverse Hyperbolic Sine: [0. 0.88137359 1.44363548]
Inverse Hyperbolic Cosine: [1.3169579 1.76274717 2.09471255]
Inverse Hyperbolic Tangent: [ 0.54930614 -0.54930614]Example 3: Relationship Between Hyperbolic Functions
Hyperbolic functions satisfy mathematical identities, such as:
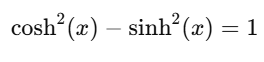
Let’s verify this with NumPy:
# Verify the identity cosh^2(x) - sinh^2(x) = 1
x = np.array([0, 1, 2])
cosh_squared = np.cosh(x) ** 2
sinh_squared = np.sinh(x) ** 2
identity = cosh_squared - sinh_squared
print("cosh^2(x) - sinh^2(x):", identity)Output:
cosh^2(x) - sinh^2(x): [1. 1. 1.]Example 4: Plotting Hyperbolic Functions
You can visualize hyperbolic functions using Matplotlib.
import matplotlib.pyplot as plt
x = np.linspace(-2, 2, 100)
# Compute hyperbolic functions
sinh = np.sinh(x)
cosh = np.cosh(x)
tanh = np.tanh(x)
# Plot
plt.plot(x, sinh, label="sinh(x)", color="blue")
plt.plot(x, cosh, label="cosh(x)", color="orange")
plt.plot(x, tanh, label="tanh(x)", color="green")
plt.title("Hyperbolic Functions")
plt.xlabel("x")
plt.ylabel("Value")
plt.legend()
plt.grid()
plt.show()
Applications of Hyperbolic Functions
- Physics: Used in theories of relativity and hyperbolic motion.
- Engineering: Designing suspension bridges (catenary curves) and waveforms.
- Mathematics: Solving equations involving exponential growth and decay.
- Data Science: Modeling growth curves and transformations in neural networks.
Summary
NumPy’s hyperbolic functions provide a robust toolkit for handling mathematical computations involving hyperbolic equations and transformations. From basic hyperbolic sine to advanced inverse functions, these utilities are essential for scientific, engineering, and data applications.
For more coding tutorials and tips, visit The Coding College and take your programming skills to the next level!