Welcome to The Coding College, where we break down complex programming concepts into simple, actionable tutorials. In this guide, we’ll cover logarithmic functions in NumPy, explore their practical use cases, and show how to perform log calculations with examples.
What are Logarithms?
A logarithm is the inverse of an exponential function. For example, if:

In NumPy, logarithmic operations are performed using base-e (natural log), base-2, base-10, or custom bases.
Why Use NumPy for Logs?
- Efficiency: NumPy operates on arrays, making log computations for large datasets faster than standard Python loops.
- Variety: Functions for different log bases are available.
- Flexibility: Handles multi-dimensional arrays and broadcasting seamlessly.
NumPy Logarithmic Functions
NumPy provides the following logarithmic functions:
np.log()– Natural log (base-e)np.log10()– Common log (base-10)np.log2()– Binary log (base-2)np.log1p()– Natural log of (1 + x)
1. Natural Log (np.log)
The natural log computes logarithms with base-e (Euler’s number ≈ 2.718).
Syntax:
numpy.log(x)- x: Input array or scalar.
- Returns: Element-wise natural log.
Example:
import numpy as np
# Input array
array = np.array([1, np.e, 10, 100])
# Natural log
result = np.log(array)
print("Natural Log:", result)Output:
Natural Log: [0. 1. 2.30258509 4.60517019]2. Common Log (np.log10)
The common log computes base-10 logarithms, commonly used in scientific and financial calculations.
Syntax:
numpy.log10(x)Example:
# Base-10 log
result = np.log10(array)
print("Common Log (base-10):", result)Output:
Common Log (base-10): [0. 0.43429448 1. 2.]3. Binary Log (np.log2)
The binary log computes base-2 logarithms, often used in computer science (e.g., analyzing algorithms).
Syntax:
numpy.log2(x)Example:
# Base-2 log
result = np.log2(array)
print("Binary Log (base-2):", result)Output:
Binary Log (base-2): [0. 1. 3.32192809 6.64385619]4. Natural Log of (1 + x) (np.log1p)
np.log1p(x) computes the natural log of 1+x1 + x, which is more accurate for small values of xx compared to np.log(1 + x).
Syntax:
numpy.log1p(x)Example:
# Log of (1 + x)
small_values = np.array([0.0001, 0.001, 0.01])
result = np.log1p(small_values)
print("Log of (1 + x):", result)Output:
Log of (1 + x): [9.99950003e-05 9.99500333e-04 9.95033085e-03]Handling Negative or Zero Values
Logarithms are undefined for zero and negative numbers. If your array contains such values, NumPy will return -inf (negative infinity) or NaN (Not a Number).
Example:
# Array with invalid values
invalid_array = np.array([1, 0, -10])
result = np.log(invalid_array)
print("Log with invalid values:", result)Output:
RuntimeWarning: divide by zero encountered in log
RuntimeWarning: invalid value encountered in log
Log with invalid values: [ 0. -inf nan]Applying Custom Logarithmic Bases
If you need a log with a custom base b:
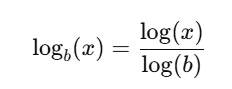
Example:
# Custom base (base 5)
base = 5
custom_log = np.log(array) / np.log(base)
print("Log with base 5:", custom_log)Output:
Log with base 5: [0. 0.62133493 1.43067656 2.86135312]Logarithms for Multi-Dimensional Arrays
NumPy’s log functions work seamlessly with multi-dimensional arrays.
Example:
array_2d = np.array([[1, 10], [100, 1000]])
# Base-10 log for 2D array
result = np.log10(array_2d)
print("Log of 2D Array (base-10):", result)Output:
Log of 2D Array (base-10):
[[0. 1.]
[2. 3.]]Performance Comparison
NumPy logarithmic functions outperform Python’s math library for large datasets.
Example:
import time
import math
# Large array
large_array = np.random.rand(int(1e6)) * 100
# NumPy log
start = time.time()
np.log(large_array)
print("NumPy Time:", time.time() - start)
# Python math.log (loop)
start = time.time()
[math.log(x) for x in large_array]
print("Python Loop Time:", time.time() - start)Output (Approximate):
NumPy Time: ~0.02 seconds
Python Loop Time: ~0.8 seconds Summary
Logarithmic functions are a vital part of numerical computations, and NumPy makes them simple and efficient to use. With its variety of built-in log functions and support for custom bases, you can handle any log operation with ease.
Explore more tutorials on The Coding College to deepen your programming knowledge and master libraries like NumPy!