Perceptrons are the fundamental building blocks of artificial neural networks, marking the origin of machine learning and deep learning models. Introduced in 1958 by Frank Rosenblatt, the perceptron is a type of artificial neuron used to classify data points into two categories. This article explores perceptrons, their architecture, working principles, and applications. For more in-depth coding and machine learning content, visit The Coding College.
What is a Perceptron?
A perceptron is a supervised learning algorithm used for binary classification. It mimics the functioning of biological neurons and can make decisions by learning weights assigned to input features.
Components of a Perceptron
- Inputs (x1,x2,…,xn): Represent features of the dataset.
- Weights (w1,w2,…,wn): Determine the influence of each input.
- Bias (b): Shifts the decision boundary to improve flexibility.
- Summation Function: Computes the weighted sum of inputs:
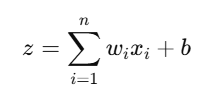
- Activation Function: Determines the output based on zz. In a perceptron, this is usually a step function:
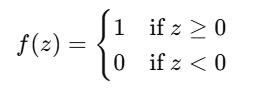
Perceptron Architecture
The perceptron architecture consists of:
- Input Layer: Accepts data points as input.
- Summation Node: Combines inputs with weights and bias.
- Output Node: Produces the final prediction based on the activation function.
How Does a Perceptron Work?
- Initialize Weights and Bias: Start with random values.
- Input Data: Pass the feature values into the perceptron.
- Compute Weighted Sum: Calculate z=∑wixi+b.
- Apply Activation Function: Determine the output (1 or 0).
- Update Weights (Learning): Adjust weights and bias using the perceptron learning rule:
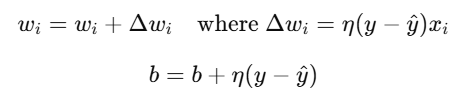
- y: Actual output.
- y^: Predicted output.
- η: Learning rate.
Limitations of Perceptrons
- Linear Separability: Perceptrons can only solve problems where the data is linearly separable, such as OR and AND gates. They fail for non-linear problems like XOR.
- Fixed Activation: The step function limits gradient-based optimization techniques.
Applications of Perceptrons
- Binary Classification
- Example: Classifying emails as spam or not spam.
- Logic Gates
- AND, OR, and NOT gates can be modeled using perceptrons.
- Feature Detection
- Simple edge detection in image processing tasks.
Perceptrons in Python
Below is a simple Python implementation of a perceptron for a binary classification task:
import numpy as np
# Step Activation Function
def step_function(z):
return 1 if z >= 0 else 0
# Perceptron Model
class Perceptron:
def __init__(self, learning_rate=0.01, epochs=1000):
self.lr = learning_rate
self.epochs = epochs
self.weights = None
self.bias = None
def fit(self, X, y):
n_samples, n_features = X.shape
self.weights = np.zeros(n_features)
self.bias = 0
for _ in range(self.epochs):
for idx, x_i in enumerate(X):
z = np.dot(x_i, self.weights) + self.bias
y_pred = step_function(z)
# Update weights and bias
update = self.lr * (y[idx] - y_pred)
self.weights += update * x_i
self.bias += update
def predict(self, X):
linear_output = np.dot(X, self.weights) + self.bias
return [step_function(i) for i in linear_output]
# Dataset: OR Gate
X = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
y = np.array([0, 1, 1, 1])
# Train Perceptron
model = Perceptron(learning_rate=0.1, epochs=1000)
model.fit(X, y)
# Predict
predictions = model.predict(X)
print("Predictions:", predictions)Moving Beyond Perceptrons: Multi-Layer Perceptrons (MLPs)
The limitations of perceptrons led to the development of multi-layer perceptrons (MLPs), which form the basis of modern neural networks. MLPs overcome non-linear problems using multiple layers and activation functions like ReLU and sigmoid.