Probability is the mathematical study of uncertainty. It measures the likelihood of an event occurring, providing a way to quantify randomness and make predictions about outcomes. From coin tosses to weather forecasts and machine learning models, probability is a cornerstone of many disciplines.
This guide explores the basics of probability, key concepts, types, formulas, and its applications.
What Is Probability?
Probability quantifies how likely an event is to happen, expressed as a value between 0 and 1:
- 0: The event is impossible.
- 1: The event is certain.
- In Between (0 to 1): Represents the likelihood of occurrence.
Formula for Probability
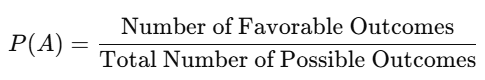
Where P(A) is the probability of event A.
Key Concepts in Probability
1. Sample Space (SS)
The set of all possible outcomes of a random experiment.
- Example: For a dice roll, S={1,2,3,4,5,6}.
2. Event (AA)
A subset of the sample space representing a specific outcome or group of outcomes.
- Example: Rolling an even number (A={2,4,6}.
3. Complementary Events
The complement of event A (A’) is the event that AA does not occur. P(A′)=1−P(A)
4. Mutually Exclusive Events
Events that cannot occur simultaneously.
- Example: Rolling a 4 and a 5 on a single dice roll.
5. Independent Events
Events where the occurrence of one does not affect the other.
- Example: Flipping two coins.
Types of Probability
1. Theoretical Probability
Based on mathematical reasoning and logic.
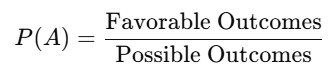
- Example: Probability of rolling a 3 on a die: P(3)=16.
2. Experimental (Empirical) Probability
Based on observation or experiment.
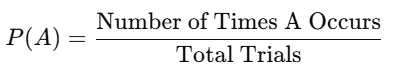
- Example: Measuring the probability of a coin landing heads after flipping it 100 times.
3. Subjective Probability
Based on personal judgment or experience, rather than mathematical calculation.
- Example: Predicting the likelihood of rain tomorrow based on intuition.
Rules of Probability
1. Addition Rule
For two mutually exclusive events A and B: P(A or B)=P(A)+P(B)
For non-mutually exclusive events: P(A or B)=P(A)+P(B)−P(A and B)
2. Multiplication Rule
For independent events AA and BB: P(A and B)=P(A)×P(B)
Examples of Probability
Example 1: Rolling a Dice
- Event AA: Rolling a 4.
- Sample Space S={1,2,3,4,5,6}.
- Probability:
P(A)=6/1
Example 2: Flipping Two Coins
- Event AA: Getting at least one head.
- Sample Space: S={HH,HT,TH,TT}.
- Favorable Outcomes: HH,HT,TH.
- Probability:
P(A)=3/4
Applications of Probability
- Finance: Calculating risk in investments.
- Healthcare: Predicting patient recovery rates.
- Machine Learning: Designing algorithms like Naive Bayes.
- Gaming: Developing fair rules and outcomes.
Example in Python
Here’s a Python snippet to calculate probability:
from itertools import product
# Sample space for flipping 2 coins
sample_space = list(product(['H', 'T'], repeat=2))
# Event: At least one head
event = [outcome for outcome in sample_space if 'H' in outcome]
# Probability calculation
probability = len(event) / len(sample_space)
print(f"Probability of at least one head: {probability}")Visualizing Probability
- Bar Charts: Represent discrete probabilities.
- Pie Charts: Show proportions.
- Histograms: Visualize probabilities in continuous distributions.